90 60 30 üçgeni kuralı 783195-90 60 30 üçgeni kuralı

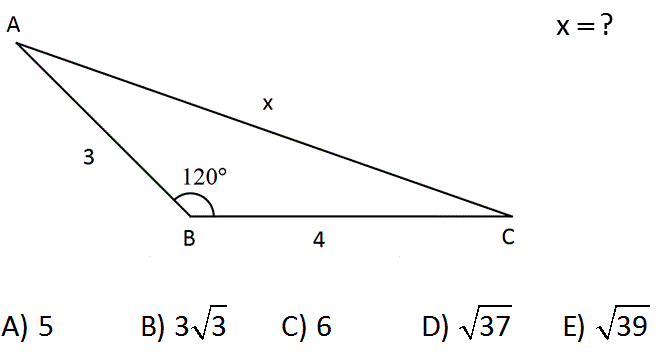
30 60 90 üçgeni kuralları bunlardan ibarettir Bu kuralların bilinmesiyle üçgende açı uzunluk ve alan hesaplama gibi bir çok konunun oldukça kolay ve A) 3 B) 4 C) 5 D) 6 E) 7 Çözüm Dik üçgeni D ve C köşelerinden uzatarak tamamlarsak; 30 60 90 üçgeni Olay çok basit öncelikle dik üçgeni tanıyalım Dik üçgen olması için zaten üçgenin açılarından biri 90 derece olmalı Önce bu 90 derecelik açıyı bulun bu açının karşısındaki kenara hipotenüs adı verilir ve bu kenar dik üçgenin en uzun kenarıdır

Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu

90 60 30 üçgeni kuralı

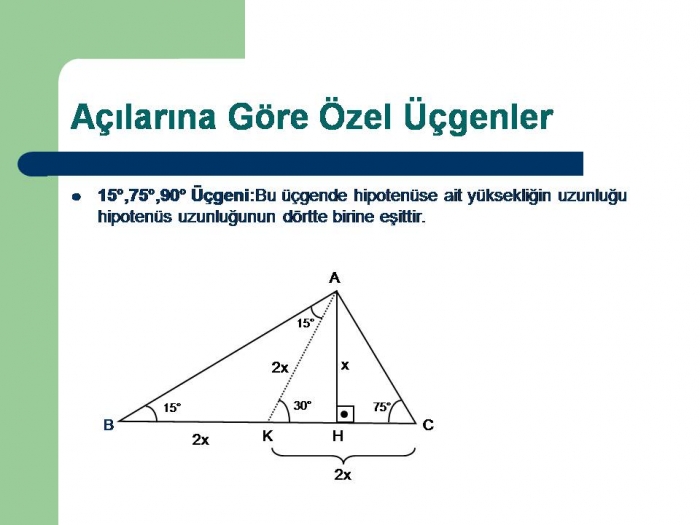
90 60 30 üçgeni kuralı-Bu ders notumuzda Geometri dersinin Özel Üçgenler başlığı altında; Öğretmenlerinizin 'şuradan bir dikme indir', 'buradan bir çizgi çek' dediği yerler aslında üçgeni bulmanız içindir 30 60 90, 45 45 90, 30 30 1 gibi bir tane de 15 75 90 üçgeni vardır Gelin 15 75 90 üçgeni özellikleri nasılmış, hep birlikte öğrenelim 15 75 90 Üçgeni Özellikleri

15 75 90 Ucgeni Not Bu

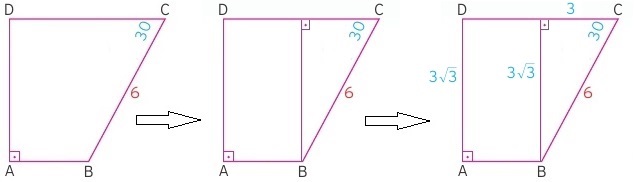
 Geometride karşımıza çıkan özel dik üçgenler bulunmaktadır Bu özel dik üçgenlerden bir tanesi ise 30 60 90 üçgenidir Bu 30 60 90 üçgeni bir eş üçgenin yükseklik ile iki eş parçaya bölünmesinden oluşmuştur Bu üçgenin açıları 30 derece 60 derece ve 90 derecedir Bu açıları gören kenarların uzunluklarının ise belirli bir kuralı bulunmaktadır 30 derecelik Zik Zak Kuralı Nedir ?A) 2 2 B) 2 3 C) 3 2 D) 4 2 E) 6 Çözüm wwwmatematikkolaynet Üçgeni dışardan 45 45 90 üçgeni olacak şekilde uzatalım Büyük üçgen 30 60 90 üçgeni olur 90 'nin karşısında 6 2 var sa 30 nin karşısında yarısı olur 6 2 3 2 dir 2 45 45 90 üçgeninde 45 nin karşısında 3 2 var sa;

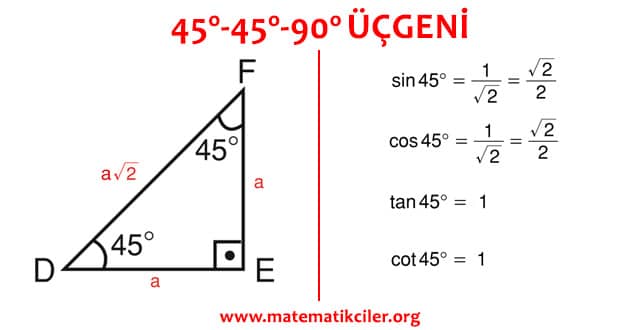
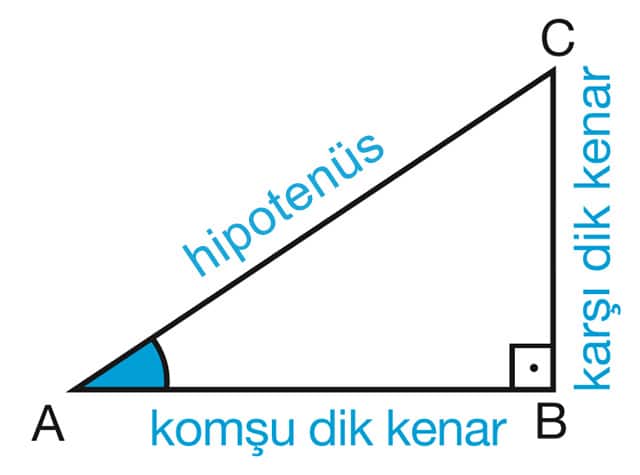
 45 45 90 Üçgeni, özel üçgenlerden biri olup, geometri dersinde çok önemli bir yeri bulunmaktadır Trigonometrik bağıntıları çok iyi idrak etmek için 45 45 90 üçgenini çok iyi bilmek gerekir Bu nedenle, bu üçgeni çok iyi bilmek karşılaşılacak tüm soruların kol  Üçgeni Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittir Açıortay C açısını tam ortasından 30°'lik iki eşit parçaya bölerken, kenarortay da AB doğru parçasını tam ortasından iki eşit parçaya ayırır 30 60 90 üçgeni kuralı Yukarıdaki eş kenar üçgeni iki eşit parçaya ayırdığımızda elde ettiğimiz üçgene " Üçgeni" denir

Son Yüklenen Görüntüler Arşivler Arşivler Etiketler Antalya (1021) bir (1051) DHA (3218) GÜNCEL Haberleri (1719) GÜNDEM HABERLERİ () güncel ()15 75 90 özel üçgeni özellikleri ve örnek sorular Giriş Tarihi 1521 1536 Son Güncelleme 1521 1545 Haberler Eğitim Haberleri 15 75 90 üçgeni kuralı nedir ?

Angle And Trigonometric Functions 11 10 Sideway Output To

En Hizli 30 60 90 Ucgeninin Kurali

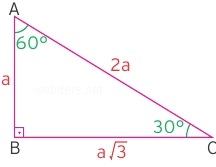
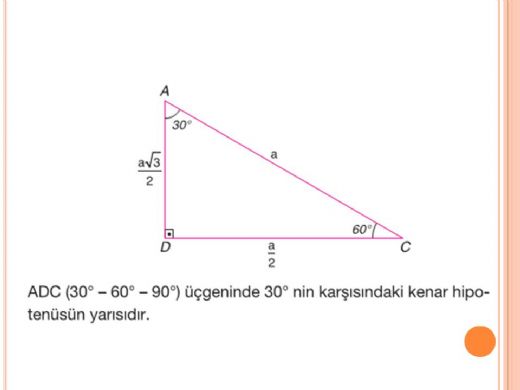
(30° 60° 90°) dik üçgeninde;Z Kuralı Nedir ?30°'lik açının karşısındaki kenar hipotenüsün yarısına eşittir 60°'lik açının karşısındaki kenar, 30° nin karşısındaki kenarın 3 katıdır

30 60 90 Ucgeni Basit Bir Soru Yapabilirsiniz Eodev Com

Dik Ucgen Vikipedi

 30 60 90 üçgeni ile ilgili soruları zaten çoğunlukla bu şekilde görürüz Yani karşımıza üçgeni çıkarıp bize basit soru sormazlar Bunu elde etmemizi isterler 30 60 90 üçgeni kuralları bunlardan ibarettir Bu kuralların bilinmesiyle üçgende açı uzunluk ve alan hesaplama gibi bir çok konunun oldukça kolay ve kısa yoldan çözülür Bu kuralların bilinmesiyle üçgende açı uzunluk ve alan hesaplama gibi bir çok konunun oldukça kolay ve kısa yoldan çözülürDoğruların Oluşturduğu Açılar 1 Ters Açılar İki doğrunun kesişmesiyle oluşan açılardır Ölçüleri eşittir 2 Paralel İki Doğrunun Bir Kesenle oluşturduğu Açılar I) Yöndeş Açılar

Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali

Dik Ve Ozel Ucgenler 1

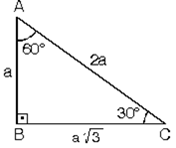
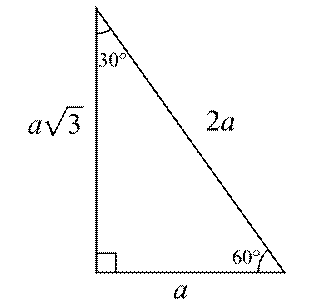
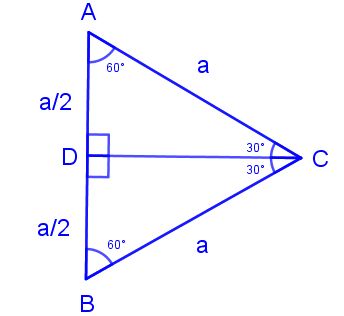
üçgeni üçgeni ve ispatı Açıları olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardırBCaa2a3(30,60,90) dik üçgeni(300,600,900) üçgeninde 300lik açının karşısındaki kenarın uzunluğu hipotenüsün yarısına, 600lik açının karşısındaki kenarın uzunluğu ise hipotenüsün yarısının katına eşittir yada 300lik açının katı diyebilirizÖrnekAACABC dik üçgeninde c açısının ölçüsü 30 30 1 üçgeni 30 30 1 üçgeni bir ikizkenar üçgendir 1 derecelik açının karşısından karşı kenara dikme indirdiğinizde iki tane eş 30 60 90 üçgeni elde ederiz Yamuk sorularında Yamuk sorularında dikme indirdiğimiz zaman 30 60 90 üçgeni karşımıza çok çıkmaktadırYine aynı oranlarla kenarları bulmak ve alan hesaplamak kolay olacaktır

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt

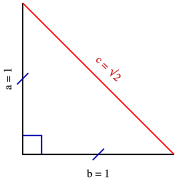
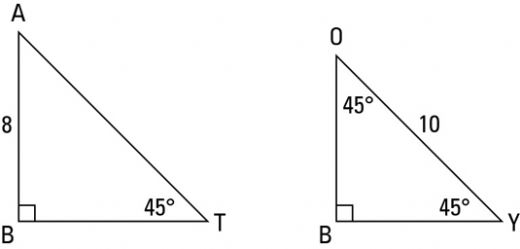
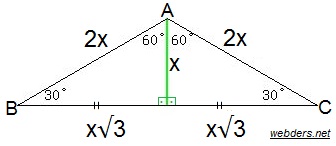
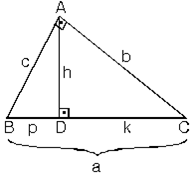
Veya 2 x eşittir 90 iki tarafı da 2'ye bölersek, x'i 45 derece olarak buluruz İkizkenar dik üçgenin daha sıklıkla kullanılan ismi, üçgenidir Bir önceki video da üçgeni için yaptığımız gibi, bu videoda bu sefer üçgeninin kenar oranlarını bulmak istiyorum 30 – 30 – 1 ikizkenar üçgeni iki adet 30 – 60 – 90 dik üçgeninden oluşur 1 0 'nin karşısındaki kenar ikiz kenarların √3 katına eşittir Dik Üçgen ve Öklid Kuralları Dik üçgenlerde 90°'lik açının bulunduğu köşeden hipotenüse bir dikme inilmişse iki yeni dik üçgen oluşurU Kuralı Nedir ?

30 60 90 Ucgeni Pow Bylge

Indirim Kurali I Ngiliz Sistemi Metrik Sistem Ucgen Kural 90 Genis Alt Kalinlasmak Aluminyum Alasimli Marangoz Kare 45 Aci Kare Olcum Ve Analiz Cihazlari Pazarogeleri News

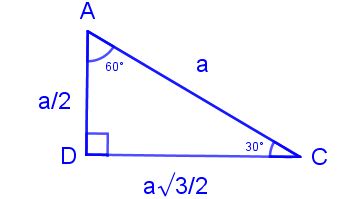
ABE üçgeninde 30 ve 90 derece duruyor, burada o zaman bu karşıdaki açı da 60 derece olmalı Yani buradaki AEB açısı da 60 olmalı BCD üçgeninde de 30 derecemiz var, 90 derecemiz var 180'e tamamlamak için burası 60 derece olmalı Ve işte ilk 306090 nin karşısında 2 katı olur Ya da sin1 = √3 / 2 formülü size yardımcı olabilecek farklı bir yöntem Eğer bu yöntemler aklınıza gelmezse bu durumda tepe açısından bir dikme indirmeniz işinizi kolaylaştıracaktır Bu sayede iki adet eş 30 60 90 üçgeni oluşturursunuz ki bunun bütün özelliklerinden yararlanabilirsiniz

Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger Hepsi Konu Anlatimi

Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com

(30 60 90) Üçgeni (30 30 1) Üçgeni Eşkenar Üçgen (30 30 1) Üçgeni (30 30 1) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz ) 30 60 90 Üçgeni Kuralı Nedir?Dik Üçgen, Pisagor Bağıntısı, Özel Dik Üçgenler, İkizkenar dik üçgen, (30° – 60° – 90°) Üçgeni, (30° – 30° – 1°) Üçgeni, (15° – 75° – 90°) Üçgeni, Öklit Bağıntıları, İkizkenar Üçgen, Eşkenar Üçgen vb içerikler hakkında detaylı bilgileri bulabilirsiniz

How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies

15 75 90 Ucgeni Not Bu

Kuvvetler üçgeni triangle down leg triangle acute triangle perpendicular bisector of side inscribed triangle triangle obtuse triangle incenter, inscribed circle 345 triangle right isosceles triangle balance point isosceles triangle median circumcenter, circumscribed circleQuote Orijinalden alıntı brknzbz üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve üçgeni oluşturmak(30 60 90 üçgeni kuralı) A 4cm B 4 C D 60° E m (BDE) paralellik kuralından 60° olur A m (ABD) paralellik kuralından 60° olur A A m (BAE) = a olursa m (FED) = a derece olur A (ACE) ikizkenar üçgen olduğu ortaya çıkar z o £2 Q LU 7 4V3

Find The Value Of X In The Adjoining Figure Img Src D10lpgp6xz60nq Cloudfront Net Physics Images Ps Sci Vi C05 S01 007 Q01 Png Width 80

Ucgen Kural 90 Derece Kalinlasma Aci Kural Aluminyum Alasim Marangoz Olcum Kare Cetvel Uygun Fiyatli Satin Alin Fiyat Ucretsiz Teslimat Fotograflarla Gercek Yorumlar Joom

Kalem Ucu Kuralı Nedir ? özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeniÜçgeni Kenar uzunlukları (3 – 4 – 5) sayıları veya bunların katı olan bütün üçgenler dikÜçgeni ile İlgili Soru Geri Üçgeni ile İlgili Soru KhanAcademyTurkce 511K subscribers Subscribe

45 45 90 Ucgeni Turleri Ve Ozellikleri

En Hizli 30 60 90 Ucgeninin Kurali

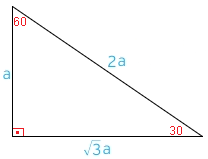
Kenarlar sırasıyla a, a√3 ve 2a olur 30 un karşısındaki kenar a 60 ın karşısındaki kenar a√3 (30 dakinin √3 katı) 90 ın karşısındaki kenar 2a (30 daki kenarın 2 katı) uygulama bölümü ise 30,60 yada 90 ın karşısındaki bir kenar verilir veE açısı 30 olur CDE üçgeni 30 – 1 – 30 üçgeni olur 30 'nin karşısında a var sa 1 'nin karşısında a 3 olur CE 3 3 3 br olur ABE üçgeninde BE 8 br old uğuna göre 8 AB 4 br olur (3090 60 30 üçgeni kpss konu anlatımı

30 60 90 Ucgeni Webders Net

15 75 90 Ucgeni Webders Net

 – İç açıları her daim kural doğrultusunda üçgeni olarak bilinir – Bir dik üçgendir – 30 derecenin karşısında olan kenar hipotenüsün yarısıdır30 60 90 Üçgeninin Özellikleri Nelerdir? İkizkenar üçgen hakkında bildiğiniz bütün özellikler, 30 30 1 üçgeninde de geçerlidir 30 30 1 üçgeninin en güzel yanlarından biri de, 1 derecelik geniş açıdan tabana doğru indirilen dikme iki adet 30 60 90 üçgeni vermesidir Böylece öğrenciler soruları daha iyi çözerler ÖSYM de sınavlarda genellikle

260x185x185mm Metrik Aluminyum Alasim Ucgen Cetvel Siyah Ucgen Kural Iletki Olcegi 0 90 Derece Woodworking Machinery Parts Aliexpress

Dik Ucgende Trigonometrik Oranlar Sanatsal Egitim

15 75 90 üçgeni alan formülü 15 75 90 üçgeni 2 ayrı çözüm yöntemi bulunur bunlardan bir tanesi 75 derecelik açıyı 30 ve 45 olarak, diğeri de 15 ve 60 olarak bölmektir 30 ve 45 olarİç açıları 15 derece ve 75 derece ile 90 derece oluşan özel üçgene üçgeni denmektedir Bu üçgen aynı zamanda iç açıları kapsamındaSaat önce Göz Atın Kapalı 30 60 90 üçgeni olarak geçen bu kural hakkında öğrenciler kafasında birçok soru bulunmaktadır 30 60 90 üçgeninin kuralı nedir, özellikleri nelerdir gibi sorular öğrencilerin merak

15 75 90 Ucgeni Uludag Sozluk

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

(30° – 60° – 90°) Üçgeni Geometri Konuları TYT Geometri TYT Geometri Konuları Oku Üçgenlerde Uzunluk Üçgenlerde Uzunluk 17 Ocak 12 16 Ocak 12 xMaTeMaTiK 0 yorum (15° 75° 90°) Üçgeni, (3 4 5) L Hospital Kuralı (1) Limit ve Süreklilik (1) Logaritma (1)Read özel üçgenler (30°60°90° üçgeni) from the story Matematik Formülleri by TheMuhammedALI with 2,101 reads wattys15, formüller, geometri Resime bakınM Kuralı Nedir ?

Dik Ucgen Vikipedi

En Hizli 30 60 90 Ucgeni Kurallari

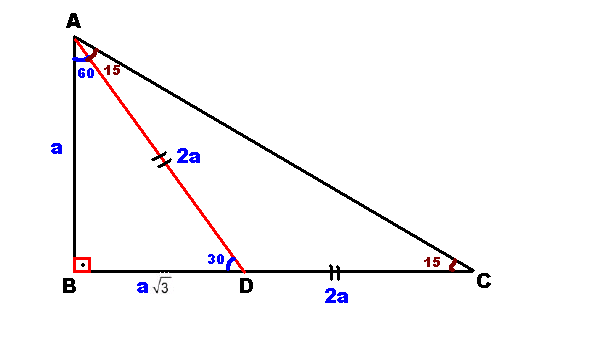
 30 60 90 Üçgeni Kuralı Nedir?  Üçgeni (2√3) İSPAT 15⁰'nin karşısına a diyelim Şekildeki gibi iki üçgene ayırırsak (0) ve () lABl=a ise lBDl=a√3 olacaktır ve lDCl=2a olur lABl=a√32a = a (2√3) olacaktır Facebook yorumcularımız FacePost(30 60 90) Üçgeni (30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz

Dik Ucgende Trigonometrik Oranlar

Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim

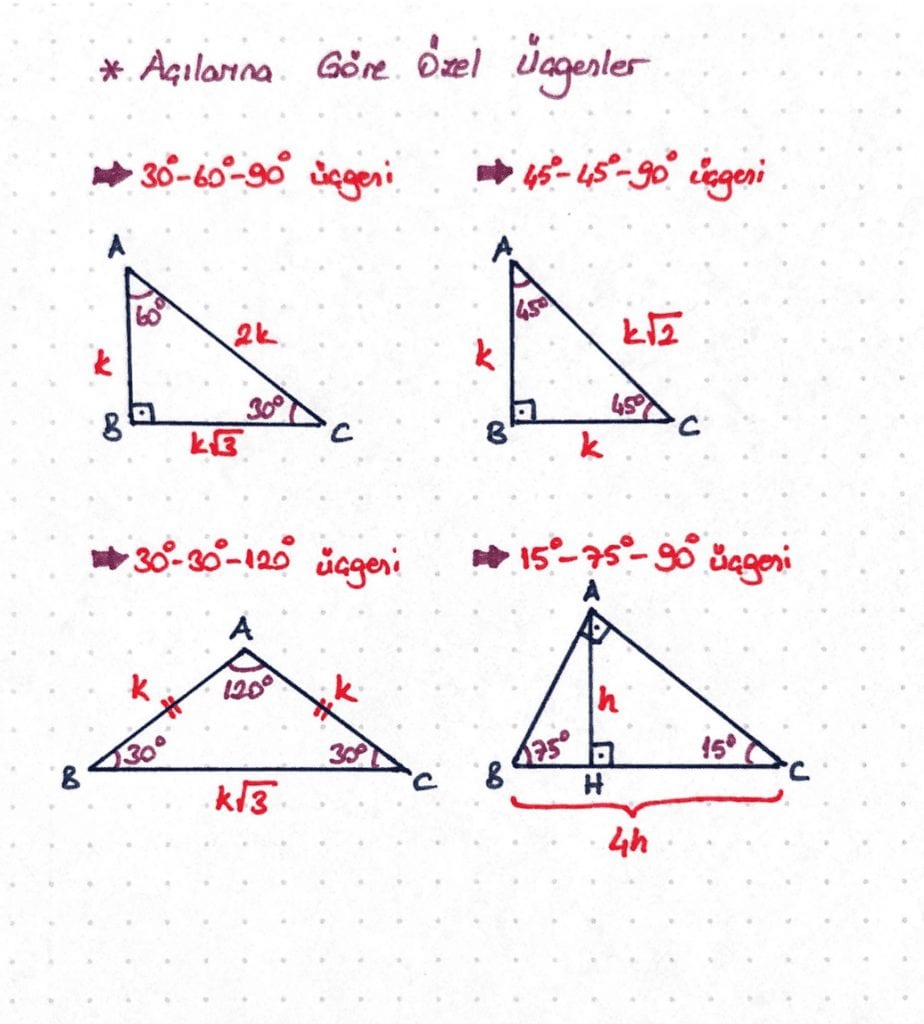
Özel Dik Üçgenler 1 ÜÇGENİ; Dik üçgen olan 30 60 90 üçgeninin hemen yanına 60 derece içinden 15 derece daha açı tamamlayarak bir doğru parçası çekerseniz üçgen genişler ve siz yine 15 75 90 üçgeni ortaya çıkartmış olursunuz  İç açıları her daim kural doğrultusunda üçgeni olarak bilinir Bir dik üçgendir 30 derecenin karşısında olan kenar hipotenüsün yarısıdır 60 derecenin karşısında olan kenar 30 dereceyi gören kenarın kök 3 katıdır

Dik Ucgende Trigonometrik Oranlar Sanatsal Egitim

Geometri Formulleri Sezgin Oner Matematik Yayinlari Facebook

Üçgeni Kenar Oranları İspatı Geri Üçgeni Kenar Oranları İspatı KhanAcademyTurkce 509K subscribers SubscribeÖzel Dik Üçgenler 1 ÜÇGENİ; yarasa kuralı kural kural pisagor teorimi özel üçgenler (30°60°90° üçgeni) özel üçgenler (15°75°90° üçgeni) öklit teorimi

45 45 90 Ucgeni Matematikce

30 30 1 Ucgeni Kurali Nedir 30 30 1 Ozel Ucgeni Ozellikleri Ve Ornek Sorular

 Araştırmada yer alan NASA yetkilileri de elde edilen bulguların, kainatın ve kainatın karmaşık yapısının kafaları karıştıran geçmişine ilişkin daha derin bir kavrayış getirdiğini belirtti (AA / 21 Mart 13) wwwakademikfiziknet Gönderen Çeşitli Blog zaman 0654 Hiç yorum yok30 60 90 Üçgeninin Özellikleri Nelerdir? 45 45 90 üçgeni de işimizi kolaylaştıracak özel üçgenlerden biridir 45 45 90 üçgenini iyi öğrenirsek temel bazı trigonometrik bağıntıları da öğrenmiş oluruz Bu nedenle bu üçgeni ve özelliklerini bilmek önemlidir Öncelikle en az bu üçgen kadar önemli 30 60 90 üçgeni olduğunu belirtelim Bu özel üçgenle

30 30 1 Ucgeni Soru List

Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com

Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik

1 30 30 Ucgeni Webders Net

5 Soru 30 60 90 Ucgeni Youtube

Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu

Nereden Cikti Bu 30 60 90 Ucgeni 30 60 90 Ucgeni Ispati Youtube

Find The Value Of Each Variable Please Help Me Brainly Com

Daha Fazlasi Icin Takip Etmeyi Unutmayin Yks Ayt Ayt21 Tyt Tyt Tyt21 Kpss Kpss21 21 Ayrik Matematik Ders Calisma Ipuclari Evde Egitim

Dik Ve Ozel Ucgenler 1

En Hizli 30 60 90 Ucgeninin Kurali

Ozel Ucgenler Dik Ucgen Ikizkenar Ucgen Eskenar Ucgen

15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz

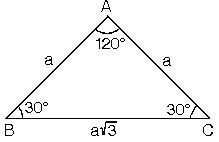
Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

Trigonometri 30 60 90 Ve 45 45 90 Ucgenleri Ile Trigonometrik Oranlari Youtube

Electronics Free Full Text Machine Learning And Lpwan Based Internet Of Things Applications In Healthcare Sector During Covid 19 Pandemic Html

30 60 90 Ucgeni

30 60 90 Ucgeni Nedir Ozellikleri Nelerdir Nasil Hesaplanir En Son Haberler Milliyet

Haos Dfybrpuvm

30 60 90 Ucgeni Akilli Geometri

2

30 60 90 Ucgeni Pisagormatik

Ozel Dik Ucgen Hipotenus Dik Aci Aci Aci Beyaz Metin Png Pngwing

30 60 90 Ucgeni Webders Net

Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali

Arkadaslar Yardimci Olur Musunuz 45 60 75 75 In Ordan Dik Indirdim Yine 45 30 A Ayirdim Ama Bulamadim Eodev Com

Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube

15 75 90 Ucgeni 2 3 Ispat

30 60 90 Ucgenleri 11 Sinif Matematik Khan Academy Turkce

30 30 1 Ucgeni Not Bu

15 75 90 Ucgeni Ozellikleri Ve Kurallari

En Hizli 30 60 90 Ucgeni Kurali

30 60 90 Ucgeni Ibrahim Hocca

30 60 90 Ucgeni

30 60 90 Ucgeni Ve Bagintilari Formulleri 8 Sinif Matematik 15 16

30 60 90 Ucgeni

30 60 90 Ucgeni Matematik Geometri Ve Turkce Blogu Dgs Ales Kpss

Ozel Dik Ucgenler Sanatsal Egitim

70 90 Ucgeni Hd Png Download Transparent Png Image Pngitem

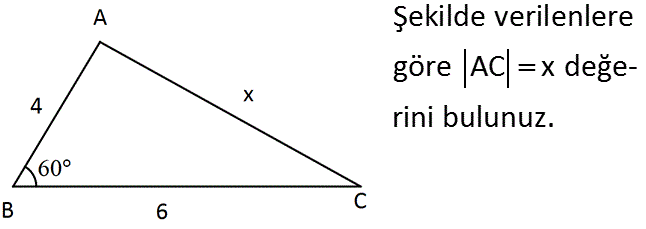
30 60 90 Ucgeni

30 60 90 Ucgeni Ile Ilgili Soru Lutfen Cozumlu Olsun Eodev Com

30 60 90 Ucgeni Kurali Nedir 30 60 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Son Dakika Egitim Haberleri

45 45 90 Ucgeni Matematikce

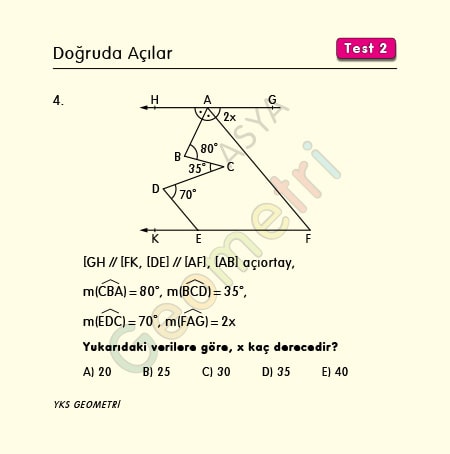
Angles On A Straight Line Test 2 Course Geometry

30 60 90 Ucgeni Ibrahim Hocca

Matematik Formulleri Ozel Ucgenler 30 60 90 Ucgeni Wattpad

30 60 90 Ucgeni Ve Ozellikleri Not Bu

30 60 90 Ucgeni Youtube

Dik Ucgende 30 Un Karsisi 3 Ise 60 Ve 90 In Karsisi Ne Olur Eodev Com

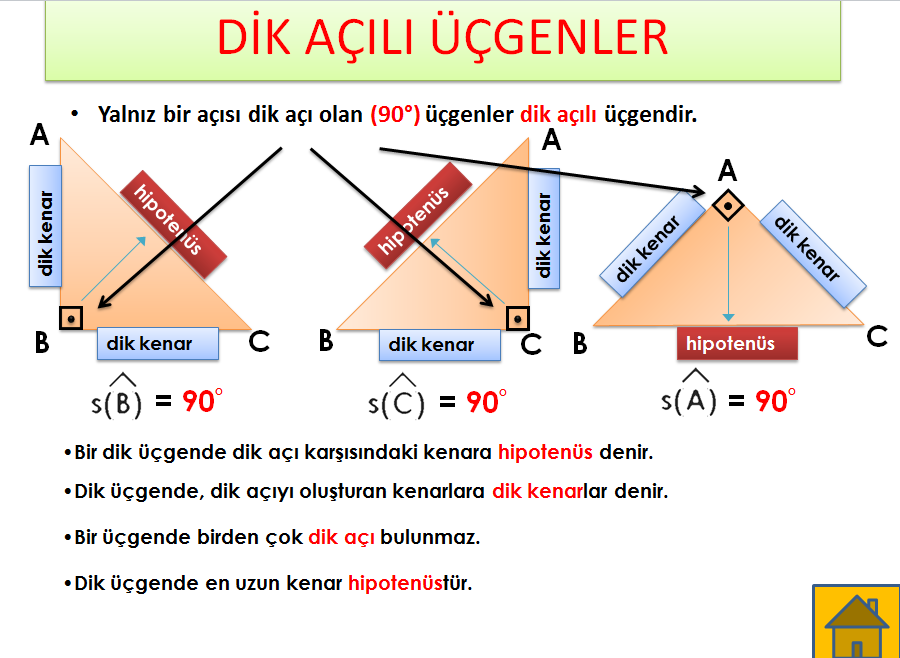
Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

90 60 30 Ucgeni

Zoqr8sxmfxasqm

30 60 90 Ucgeni Ibrahim Hocca

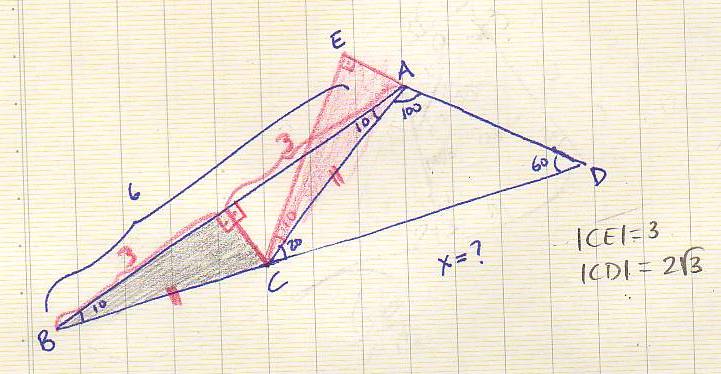
Geometri Sorusu Donanimhaber Forum

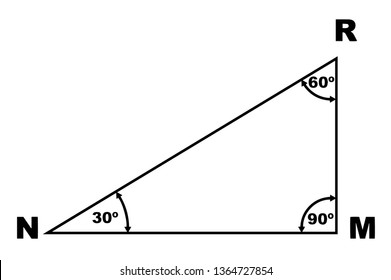
60 Degrees Triangle Images Stock Photos Vectors Shutterstock

Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali

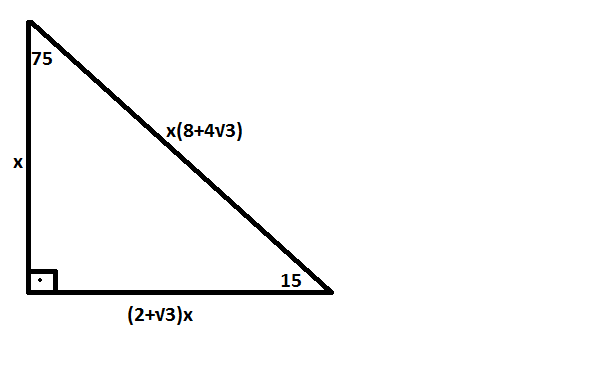
15 75 90 Ucgeni Uludag Sozluk

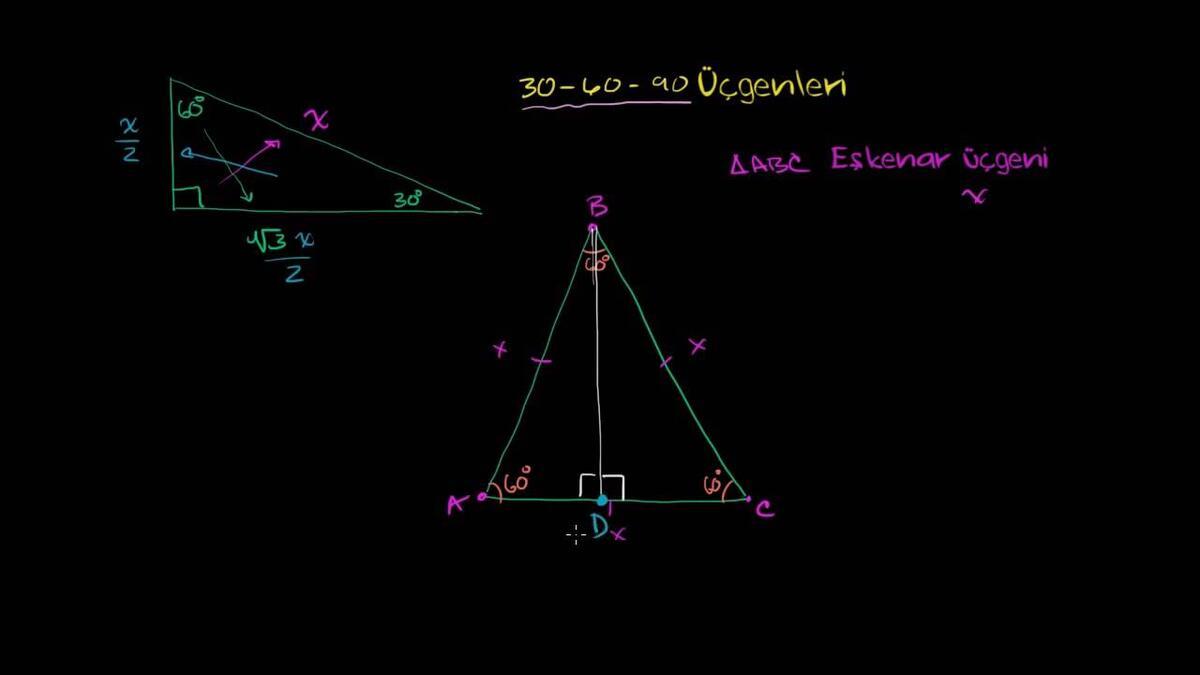
30 60 90 Ucgeni Kurali Nedir 30 60 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri

Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt

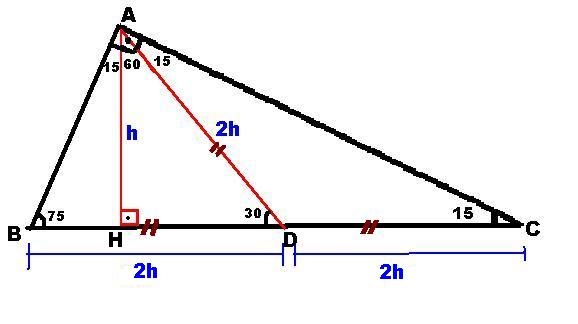
15 75 90 Ucgeni H 4h Ispat

30 60 90 Ucgeni

Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com

30 30 1 Ucgeni Not Bu

Ucgen Nasil Hesaplanir 30 60 90 Bilim 21

30 60 90 Ucgeni Turleri Ve Ozellikleri

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

Acilar Ve Ucgenler

90 60 30 Ucgeni

Incoming Term: 90 60 30 üçgeni kuralı,